本篇以數學公式說明,從連桿聯結到曲柄的非偏移活塞 運動(在內燃機 中);並且就這些運動方程式如何導出,附一示例圖。
活塞銷、曲柄銷和曲柄中心幾何布局示意圖
l
{\displaystyle l}
r
{\displaystyle r}
A
{\displaystyle A}
x
{\displaystyle x}
v
{\displaystyle v}
a
{\displaystyle a}
ω
{\displaystyle \omega }
所述曲軸的角速度,即是發動機每分鐘轉數(RPM):
ω
=
2
π
⋅
R
P
M
60
{\displaystyle \omega ={\frac {2\pi \cdot \mathrm {RPM} }{60}}}
如圖所示,曲柄銷,曲柄中心和活塞銷形成角NOP。根據餘弦定理 可以看出:
l
2
=
r
2
+
x
2
−
2
⋅
r
⋅
x
⋅
cos
A
{\displaystyle l^{2}=r^{2}+x^{2}-2\cdot r\cdot x\cdot \cos A}
以下公式描述活塞相對於曲軸轉角的往復運動。下面顯示了這些方程的示例圖。
相對於曲軸轉角的位置(通過重新排列三角關係):
l
2
−
r
2
=
x
2
−
2
⋅
r
⋅
x
⋅
cos
A
{\displaystyle l^{2}-r^{2}=x^{2}-2\cdot r\cdot x\cdot \cos A}
l
2
−
r
2
=
x
2
−
2
⋅
r
⋅
x
⋅
cos
A
+
r
2
[
(
cos
2
A
+
sin
2
A
)
−
1
]
{\displaystyle l^{2}-r^{2}=x^{2}-2\cdot r\cdot x\cdot \cos A+r^{2}[(\cos ^{2}A+\sin ^{2}A)-1]}
l
2
−
r
2
+
r
2
−
r
2
sin
2
A
=
x
2
−
2
⋅
r
⋅
x
⋅
cos
A
+
r
2
cos
2
A
{\displaystyle l^{2}-r^{2}+r^{2}-r^{2}\sin ^{2}A=x^{2}-2\cdot r\cdot x\cdot \cos A+r^{2}\cos ^{2}A}
l
2
−
r
2
sin
2
A
=
(
x
−
r
⋅
cos
A
)
2
{\displaystyle l^{2}-r^{2}\sin ^{2}A=(x-r\cdot \cos A)^{2}}
x
−
r
⋅
cos
A
=
l
2
−
r
2
sin
2
A
{\displaystyle x-r\cdot \cos A={\sqrt {l^{2}-r^{2}\sin ^{2}A}}}
x
=
r
⋅
cos
A
+
l
2
−
r
2
sin
2
A
{\displaystyle x=r\cdot \cos A+{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}
相對於曲軸轉角的速度(採用一階導數,使用鏈式法則 ):
x
′
=
d
x
d
A
=
−
r
sin
A
+
(
1
2
)
.
(
−
2
)
.
r
2
sin
A
cos
A
l
2
−
r
2
sin
2
A
=
−
r
sin
A
−
r
2
sin
A
cos
A
l
2
−
r
2
sin
2
A
{\displaystyle {\begin{array}{lcl}x'&=&{\frac {dx}{dA}}\\&=&-r\sin A+{\frac {({\frac {1}{2}}).(-2).r^{2}\sin A\cos A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}\\&=&-r\sin A-{\frac {r^{2}\sin A\cos A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}\end{array}}}
關於曲軸轉角的加速度(採用二階導數,使用鏈式法則和商法則):
x
″
=
d
2
x
d
A
2
=
−
r
cos
A
−
r
2
cos
2
A
l
2
−
r
2
sin
2
A
−
−
r
2
sin
2
A
l
2
−
r
2
sin
2
A
−
r
2
sin
A
cos
A
.
(
−
1
2
)
⋅
(
−
2
)
.
r
2
sin
A
cos
A
(
l
2
−
r
2
sin
2
A
)
3
=
−
r
cos
A
−
r
2
(
cos
2
A
−
sin
2
A
)
l
2
−
r
2
sin
2
A
−
r
4
sin
2
A
cos
2
A
(
l
2
−
r
2
sin
2
A
)
3
{\displaystyle {\begin{array}{lcl}x''&=&{\frac {d^{2}x}{dA^{2}}}\\&=&-r\cos A-{\frac {r^{2}\cos ^{2}A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}-{\frac {-r^{2}\sin ^{2}A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}-{\frac {r^{2}\sin A\cos A.(-{\frac {1}{2}})\cdot (-2).r^{2}\sin A\cos A}{\left({\sqrt {l^{2}-r^{2}\sin ^{2}A}}\right)^{3}}}\\&=&-r\cos A-{\frac {r^{2}(\cos ^{2}A-\sin ^{2}A)}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}-{\frac {r^{4}\sin ^{2}A\cos ^{2}A}{\left({\sqrt {l^{2}-r^{2}\sin ^{2}A}}\right)^{3}}}\end{array}}}
如果角速度是恆定的,那麼
A
=
ω
t
{\displaystyle A=\omega t\,}
並適用以下關係:
d
A
d
t
=
ω
{\displaystyle {\frac {dA}{dt}}=\omega }
d
2
A
d
t
2
=
0
{\displaystyle {\frac {d^{2}A}{dt^{2}}}=0}
下面的等式描述了活塞相對於時間的往復運動。如果時間域是必需的,而不是角度域,先用 ω 取代在等式噸,然後擴展為角速度如下:
單純相對於時間的位置即是:
x
{\displaystyle x\,}
相對於時間的速度(使用鏈式法則):
v
=
d
x
d
t
=
d
x
d
A
⋅
d
A
d
t
=
d
x
d
A
⋅
ω
=
x
′
⋅
ω
{\displaystyle {\begin{array}{lcl}v&=&{\frac {dx}{dt}}\\&=&{\frac {dx}{dA}}\cdot {\frac {dA}{dt}}\\&=&{\frac {dx}{dA}}\cdot \ \omega \\&=&x'\cdot \omega \\\end{array}}}
相對於時間的加速度(使用鏈式法則和乘積法則以及角速度導數):
a
=
d
2
x
d
t
2
=
d
d
t
d
x
d
t
=
d
d
t
(
d
x
d
A
⋅
d
A
d
t
)
=
d
d
t
(
d
x
d
A
)
⋅
d
A
d
t
+
d
x
d
A
⋅
d
d
t
(
d
A
d
t
)
=
d
d
A
(
d
x
d
A
)
⋅
(
d
A
d
t
)
2
+
d
x
d
A
⋅
d
2
A
d
t
2
=
d
2
x
d
A
2
⋅
(
d
A
d
t
)
2
+
d
x
d
A
⋅
d
2
A
d
t
2
=
d
2
x
d
A
2
⋅
ω
2
+
d
x
d
A
⋅
0
=
x
″
⋅
ω
2
{\displaystyle {\begin{array}{lcl}a&=&{\frac {d^{2}x}{dt^{2}}}\\&=&{\frac {d}{dt}}{\frac {dx}{dt}}\\&=&{\frac {d}{dt}}({\frac {dx}{dA}}\cdot {\frac {dA}{dt}})\\&=&{\frac {d}{dt}}({\frac {dx}{dA}})\cdot {\frac {dA}{dt}}+{\frac {dx}{dA}}\cdot {\frac {d}{dt}}({\frac {dA}{dt}})\\&=&{\frac {d}{dA}}({\frac {dx}{dA}})\cdot ({\frac {dA}{dt}})^{2}+{\frac {dx}{dA}}\cdot {\frac {d^{2}A}{dt^{2}}}\\&=&{\frac {d^{2}x}{dA^{2}}}\cdot ({\frac {dA}{dt}})^{2}+{\frac {dx}{dA}}\cdot {\frac {d^{2}A}{dt^{2}}}\\&=&{\frac {d^{2}x}{dA^{2}}}\cdot \omega ^{2}+{\frac {dx}{dA}}\cdot 0\\&=&x''\cdot \omega ^{2}\\\end{array}}}
速度的最大值和最小值都沒有在曲柄角度發生(A)加或減90°。速度最大值和最小值出現在取決於桿長(l)和半行程(r)的曲柄角上,並且對應於加速度為零(橫過水平軸)的曲柄角。
當曲柄與桿成直角時,速度最大值和最小值不一定會發生。有反例證明當曲柄角度正確時速度最大值/最小值出現的觀點。
對於 6 英吋的連桿長和 2 英吋的曲柄半徑,通過數值求解加速度過零點,可確定速度最大值/最小值在曲柄角±73.17615°處。然後使用三角正弦定律,發現曲柄角為88.21738°,桿垂直角為18.60647°。在這個例子中,顯然地曲柄和連桿之間的角度並不是直角。
總結三角形的角度 88.21738°+ 18.60647°+ 73.17615°給出 180.000°。這個反例就反駁了「速度最大值/最小值是發生在當曲柄與桿成直角時」的說法。
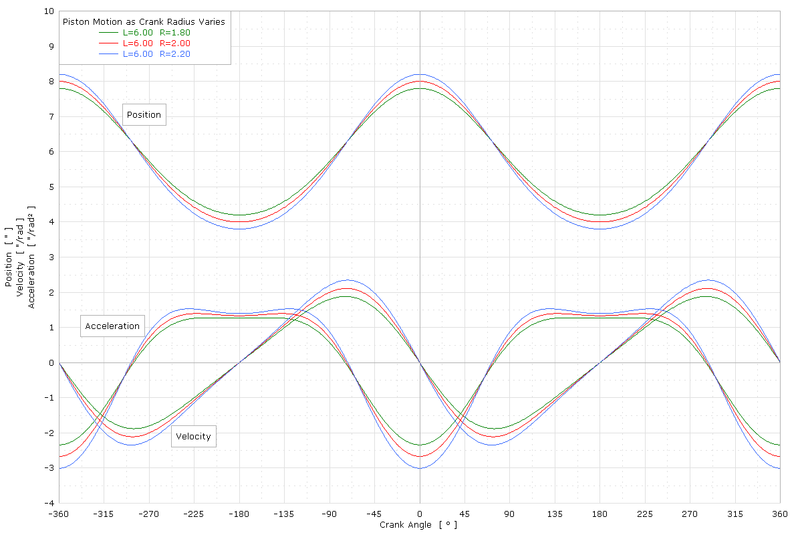
曲線圖顯示了相對於曲軸轉角的 x,x',x" 的各種半衝程,其中 L =長度(l)和 R =半行程(r):
The vertical axis units are inches for position, [inches/rad] for velocity, [inches/rad²] for acceleration.degree s.
杆長和曲柄半徑與上圖相同的活塞動畫:
活塞各半衝程動畫
John Benjamin Heywood, Internal Combustion Engine Fundamentals , McGraw Hill, 1989.
Charles Fayette Taylor, The Internal Combustion Engine in Theory and Practice, Vol. 1 & 2 , 2nd Edition, MIT Press 1985. 











![{\displaystyle l^{2}-r^{2}=x^{2}-2\cdot r\cdot x\cdot \cos A+r^{2}[(\cos ^{2}A+\sin ^{2}A)-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d70a7c30eacd6c3c5cd100f37edab327cb15972)











